Casino Theoretical Win Equation
- Casino Theoretical Win Calculation
- Casino Theoretical Win
- Casino Theoretical Win Equations
- Casino Theoretical Win Equation Generator
If you earned 20 cents in comps on another machine, that would tell you the house’s theoretical win per $100 was $3.40 and the theoretical payback was 96.6 percent. A win rate is a casino's win divided by turnover. Analysts use a 'theoretical' win rate to estimate future earnings and compare performance. Echo's theoretical win rate is about 1.6 - one of the highest in the industry - whereas Crown and SkyCity use a rate of about 1.35.
One of the most interesting aspects of blackjack is the
probability math involved. It’s more complicated than other
games. In fact, it’s easier for computer programs to calculate
blackjack probability by running billions of simulated hands
than it is to calculate the massive number of possible outcomes.
This page takes a look at how blackjack probability works. It
also includes sections on the odds in various blackjack
situations you might encounter.
An Introduction to Probability
Probability is the branch of mathematics that deals with the
likelihood of events. When a meteorologist estimates a 50%
chance of rain on Tuesday, there’s more than meteorology at
work. There’s also math.
Probability is also the branch of math that governs gambling.
After all, what is gambling besides placing bets on various
events? When you can analyze the payoff of the bet in relation
to the odds of winning, you can determine whether or not a bet
is a long term winner or loser.
The Probability Formula
The basic formula for probability is simple. You divide the
number of ways something can happen by the total possible number
of events.
Casino Theoretical Win Calculation
Here are three examples.
Example 1:You want to determine the probability of getting heads when
you flip a coin. You only have one way of getting heads, but
there are two possible outcomes—heads or tails. So the
probability of getting heads is 1/2.
You want to determine the probability of rolling a 6 on a
standard die. You have one possible way of rolling a six, but
there are six possible results. Your probability of rolling a
six is 1/6.
You want to determine the probability of drawing the ace of
spades out of a deck of cards. There’s only one ace of spades in
a deck of cards, but there are 52 cards total. Your probability
of drawing the ace of spades is 1/52.
A probability is always a number between 0 and 1. An event
with a probability of 0 will never happen. An event with a
probability of 1 will always happen.
Here are three more examples.
Example 4:You want to know the probability of rolling a seven on a
single die. There is no seven, so there are zero ways for this
to happen out of six possible results. 0/6 = 0.
You want to know the probability of drawing a joker out of a
deck of cards with no joker in it. There are zero jokers and 52
possible cards to draw. 0/52 = 0.
You have a two headed coin. Your probability of getting heads
is 100%. You have two possible outcomes, and both of them are
heads, which is 2/2 = 1.
A fraction is just one way of expressing a probability,
though. You can also express fractions as a decimal or a
percentage. So 1/2 is the same as 0.5 and 50%.
You probably remember how to convert a fraction into a
decimal or a percentage from junior high school math, though.
Expressing a Probability in Odds Format
The more interesting and useful way to express probability is
in odds format. When you’re expressing a probability as odds,
you compare the number of ways it can’t happen with the number
of ways it can happen.
Here are a couple of examples of this.
Example 1:You want to express your chances of rolling a six on a six
sided die in odds format. There are five ways to get something
other than a six, and only one way to get a six, so the odds are
5 to 1.
You want to express the odds of drawing an ace of spades out
a deck of cards. 51 of those cards are something else, but one
of those cards is the ace, so the odds are 51 to 1.
Odds become useful when you compare them with payouts on
bets. True odds are when a bet pays off at the same rate as its
probability.
Here’s an example of true odds:
You and your buddy are playing a simple gambling game you
made up. He bets a dollar on every roll of a single die, and he
gets to guess a number. If he’s right, you pay him $5. If he’s
wrong, he pays you $1.
Since the odds of him winning are 5 to 1, and the payoff is
also 5 to 1, you’re playing a game with true odds. In the long
run, you’ll both break even. In the short run, of course,
anything can happen.
Probability and Expected Value
One of the truisms about probability is that the greater the
number of trials, the closer you’ll get to the expected results.
If you changed the equation slightly, you could play this
game at a profit. Suppose you only paid him $4 every time he
won. You’d have him at an advantage, wouldn’t you?
- He’d win an average of $4 once every six rolls
- But he’d lose an average of $5 on every six rolls
- This gives him a net loss of $1 for every six rolls.
You can reduce that to how much he expects to lose on every
single roll by dividing $1 by 6. You’ll get 16.67 cents.
On the other hand, if you paid him $7 every time he won, he’d
have an advantage over you. He’d still lose more often than he’d
win. But his winnings would be large enough to compensate for
those 5 losses and then some.
The difference between the payout odds on a bet and the true
odds is where every casino in the world makes its money. The
only bet in the casino which offers a true odds payout is the
odds bet in craps, and you have to make a bet at a disadvantage
before you can place that bet.
Here’s an actual example of how odds work in a casino. A
roulette wheel has 38 numbers on it. Your odds of picking the
correct number are therefore 37 to 1. A bet on a single number
in roulette only pays off at 35 to 1.
You can also look at the odds of multiple events occurring.
The operative words in these situations are “and” and “or”.
- If you want to know the probability of A happening AND
of B happening, you multiply the probabilities. - If you want to know the probability of A happening OR of
B happening, you add the probabilities together.
Here are some examples of how that works.
Example 1:You want to know the probability that you’ll draw an ace of
spades AND then draw the jack of spades. The probability of
drawing the ace of spades is 1/52. The probability of then
drawing the jack of spades is 1/51. (That’s not a typo—you
already drew the ace of spades, so you only have 51 cards left
in the deck.)
The probability of drawing those 2 cards in that order is
1/52 X 1/51, or 1/2652.
You want to know the probability that you’ll get a blackjack.
That’s easily calculated, but it varies based on how many decks
are being used. For this example, we’ll use one deck.
To get a blackjack, you need either an ace-ten combination,
or a ten-ace combination. Order doesn’t matter, because either
will have the same chance of happening.
Your probability of getting an ace on your first card is
4/52. You have four aces in the deck, and you have 52 total
cards. That reduces down to 1/13.
Your probability of getting a ten on your second card is
16/51. There are 16 cards in the deck with a value of ten; four
each of a jack, queen, king, and ten.
So your probability of being dealt an ace and then a 10 is
1/13 X 16/51, or 16/663.
The probability of being dealt a 10 and then an ace is also
16/663.
You want to know if one or the other is going to happen, so
you add the two probabilities together.
16/663 + 16/663 = 32/663.
That translates to approximately 0.0483, or 4.83%. That’s
about 5%, which is about 1 in 20.
You’re playing in a single deck blackjack game, and you’ve
seen 4 hands against the dealer. In all 4 of those hands, no ace
or 10 has appeared. You’ve seen a total of 24 cards.
What is your probability of getting a blackjack now?
Your probability of getting an ace is now 4/28, or 1/7.
(There are only 28 cards left in the deck.)
Your probability of getting a 10 is now 16/27.
Your probability of getting an ace and then a 10 is 1/7 X
16/27, or 16/189.
Again, you could get a blackjack by getting an ace and a ten
or by getting a ten and then an ace, so you add the two
probabilities together.
16/189 + 16/189 = 32/189
Your chance of getting a blackjack is now 16.9%.
This last example demonstrates why counting cards works. The
deck has a memory of sorts. If you track the ratio of aces and
tens to the low cards in the deck, you can tell when you’re more
likely to be dealt a blackjack.
Since that hand pays out at 3 to 2 instead of even money,
you’ll raise your bet in these situations.
The House Edge
The house edge is a related concept. It’s a calculation of
your expected value in relation to the amount of your bet.
Here’s an example.
5%.
Expected value is just the average amount of money you’ll win
or lose on a bet over a huge number of trials.
Using a simple example from earlier, let’s suppose you are a
12 year old entrepreneur, and you open a small casino on the
street corner. You allow your customers to roll a six sided die
and guess which result they’ll get. They have to bet a dollar,
and they get a $4 win if they’re right with their guess.
Over every six trials, the probability is that you’ll win
five bets and lose one bet. You win $5 and lose $4 for a net win
of $1 for every 6 bets.
Your house edge is 16.67% for this game.
The expected value of that $1 bet, for the customer, is about
84 cents. The expected value of each of those bets–for you–is
$1.16.
That’s how the casino does the math on all its casino games,
and the casino makes sure that the house edge is always in their
favor.
With blackjack, calculating this house edge is harder. After
all, you have to keep up with the expected value for every
situation and then add those together. Luckily, this is easy
enough to do with a computer. We’d hate to have to work it out
with a pencil and paper, though.
What does the house edge for blackjack amount to, then?
It depends on the game and the rules variations in place. It
also depends on the quality of your decisions. If you play
perfectly in every situation—making the move with the highest
possible expected value—then the house edge is usually between
0.5% and 1%.
If you just guess at what the correct play is in every
situation, you can add between 2% and 4% to that number. Even
for the gambler who ignores basic strategy, blackjack is one of
the best games in the casino.
Expected Hourly Loss and/or Win
You can use this information to estimate how much money
you’re liable to lose or win per hour in the casino. Of course,
this expected hourly win or loss rate is an average over a long
period of time. Over any small number of sessions, your results
will vary wildly from the expectation.
Here’s an example of how that calculation works.
- You are a perfect basic strategy player in a game with a
0.5% house edge. - You’re playing for $100 per hand, and you’re averaging
50 hands per hour. - You’re putting $5,000 into action each hour ($100 x 50).
- 0.5% of $5,000 is $25.
- You’re expected (mathematically) to lose $25 per hour.
Here’s another example that assumes you’re a skilled card
counter.
- You’re able to count cards well enough to get a 1% edge
over the casino. - You’re playing the same 50 hands per hour at $100 per
hand. - Again, you’re putting $5,000 into action each hour ($100
x $50). - 1% of $5,000 is $50.
- Now, instead of losing $25/hour, you’re winning $50 per
hour.
Effects of Different Rules on the House Edge
The conditions under which you play blackjack affect the
house edge. For example, the more decks in play, the higher the
house edge. If the dealer hits a soft 17 instead of standing,
the house edge goes up. Getting paid 6 to 5 instead of 3 to 2
for a blackjack also increases the house edge.
Luckily, we know the effect each of these changes has on the
house edge. Using this information, we can make educated
decisions about which games to play and which games to avoid.
Here’s a table with some of the effects of various rule
conditions.
| Rules Variation | Effect on House Edge |
|---|---|
| 6 to 5 payout on a natural instead of the stand 3 to 2 payout | +1.3% |
| Not having the option to surrender | +0.08% |
| 8 decks instead of 1 deck | +0.61% |
| Dealer hits a soft 17 instead of standing | +0.21% |
| Player is not allowed to double after splitting | +0.14% |
| Player is only allowed to double with a total of 10 or 11 | +0.18% |
| Player isn’t allowed to re-split aces | +0.07% |
| Player isn’t allow to hit split aces | +0.18% |
These are just some examples. There are multiple rules
variations you can find, some of which are so dramatic that the
game gets a different name entirely. Examples include Spanish 21
and Double Exposure.
The composition of the deck affects the house edge, too. We
touched on this earlier when discussing how card counting works.
But we can go into more detail here.
Every card that is removed from the deck moves the house edge
up or down on the subsequent hands. This might not make sense
initially, but think about it. If you removed all the aces from
the deck, it would be impossible to get a 3 to 2 payout on a
blackjack. That would increase the house edge significantly,
wouldn’t it?
Here’s the effect on the house edge when you remove a card of
a certain rank from the deck.
| Card Rank | Effect on House Edge When Removed |
|---|---|
| 2 | -0.40% |
| 3 | -0.43% |
| 4 | -0.52% |
| 5 | -0.67% |
| 6 | -0.45% |
| 7 | -0.30% |
| 8 | -0.01% |
| 9 | +0.15% |
| 10 | +0.51% |
| A | +0.59% |
These percentages are based on a single deck. If you’re
playing in a game with multiple decks, the effect of the removal
of each card is diluted by the number of decks in play.
Looking at these numbers is telling, especially when you
compare these percentages with the values given to the cards
when counting. The low cards (2-6) have the most dramatic effect
on the house edge. That’s why almost all counting systems assign
a value to each of them. The middle cards (7-9) have a much
smaller effect. Then the high cards, aces and tens, also have a
large effect.
The most important cards are the aces and the fives. Each of
those cards is worth over 0.5% to the house edge. That’s why the
simplest card counting system, the ace-five count, only tracks
those two ranks. They’re that powerful.
You can also look at the probability that a dealer will bust
based on her up card. This provides some insight into how basic
strategy decisions work.
| Dealer’s Up Card | Percentage Chance Dealer Will Bust |
|---|---|
| 2 | 35.30% |
| 3 | 37.56% |
| 4 | 40.28% |
| 5 | 42.89% |
| 6 | 42.08% |
| 7 | 25.99% |
| 8 | 23.86% |
| 9 | 23.34% |
| 10 | 21.43% |
| A | 11.65% |
Perceptive readers will notice a big jump in the probability
of a dealer busting between the numbers six and seven. They’ll
also notice a similar division on most basic strategy charts.
Players generally stand more often when the dealer has a six or
lower showing. That’s because the dealer has a significantly
greater chance of going bust.
Summary and Further Reading
Odds and probability in blackjack is a subject with endless
ramifications. The most important concepts to understand are how
to calculate probability, how to understand expected value, and
how to quantify the house edge. Understanding the underlying
probabilities in the game makes learning basic strategy and card
counting techniques easier.
by Steve Bourie
The Seminole Tribe of Florida has six casinos in the state: Seminole Hard Rock Hotel & Casino-Tampa; Seminole Hard Rock Hotel & Casino-Hollywood; Seminole Casino-Coconut Creek; SeminoleClassic Casino-Hollywood; Seminole Casino-Brighton; and Seminole Casino-Immokalee.
All of their casinos offer slot machines and five of them also offer blackjack, as well as other kinds of house-banked card games. According to the Miami Herald, it was estimated those casinosgenerated about $2.3 billion in profits in 2016 http://www.miamiherald.com/entertainment/article166085722.html. Since the average U.S. casino generates about 65% of its profits from its electronic gaming machines, it would be fair toestimate that the Tribe’s machines earn about $1.5 billion a year for them.
The only other competition for the Tribe’s casinos are the eight local pari-mutuels in Miami-Dade and Broward Counties which all offer slot machines, but are not allowed to offer live tablegames, such as blackjack. All of these pari-mutuel casinos, also known as racinos, are in competition with the Seminole’s three Broward county casinos, but the Seminole Hard Rock Hotel& Casino in Hollywood alone generates more profits than all eight of the racinos combined.
Florida gaming regulations require all of the pari-mutuel casinos to report how much their slot machines actually pay back to the public. This “Average Payout Percentage” information isavailable to the public and can be seen on the state’s website at http://www.myfloridalicense.com/dbpr/pmw in the “Slot Revenues” section. Additionally, each racino must post a sign in the casino showing the average monthly payback percentage forall of their gaming machines. Usually, the average for all of the casinos is around 92.5%
The Seminoles are not required to release information on the payout percentages for any of their casinos and they keep this information a closely guarded secret. They say that theirmachines pay out at a rate comparable to the pari-mutuels, but no one knows for sure, and the topic is sometimes a source of controversy.
If you read reviews of Seminole casinos on Yelp, Tripadvisor, or on our website at americancasinoguide.com you will see some reviewers say they believe the machines are set to around 60%, orlower. As someone who has written about casino gambling for more than 25 years, I know that isn’t true. The procedure for deciding what a slot machine is set to pay back to the public is rathersimple. When a casino orders a slot machine the manufacturer will offer them a choice of chips to put in the machine and that chip is what controls the long-term payback percentage in thatmachine. Generally, there are about six to eight different chips to choose from and the payback percentages can be as high as 98 percent to as low as 82 percent.
Casinos, almost universally, put the highest-paying chips in the highest denomination machines and the lowest-paying chips in the lowest denomination machines. This means that $25 slots willhave chips returning around 95-98 percent and the penny machines will have chips returning around 86-89 percent.
The lowest payback I ever heard of for a chip was about 80 percent, so I knew that the 60 percent number in the user reviews was not correct, but could there be some way to find out what themachines at the Seminole casinos really paid back to the public? After a lot of research, I believe that I have correctly calculated this information and what follows is my story of how I didit, plus a simple formula to show how anyone can do it. Additionally, we’ll take a look at the returns on some specific machines at some Seminole Casinos and see how they compare to the returnsat other casinos. Now, in order to start this discussion properly, you’ll first need some background information on how casinos work.
When discussing how casinos make money, it is important to know the term “theo,” which is short for theoretical. This is how a casino expects to make money on its games. It’s referred to as“theo” because it is a theoretical number that is not guaranteed. However, the casino knows that the longer you play, the more likely your loss will approach the theoretical win for thatparticular game.
As an example, if you play a slot machine that has a 10% theo, then the casino would expect to keep about 10% of all the money you play through that machine. So, if you played $1,000 throughthat slot machine, the casino would calculate its theoretical win as $100 because 10% of $1,000 is $100. Now, since this is gambling, anything can happen when you play that machine. You may win$600, or you may lose $400 and, actually, the casino itself doesn’t know what will happen. All they know is that as long as people continue to play that machine, the casino will end up keepingabout 10% of the money that goes through that machine because the machine has a “theo” of 10%.

In order for a casino to calculate your total theo for your visit, and what you are worth as a player to them, your play must be tracked and that is done by the player’s club at each casino.All casinos have a player’s club where visitors can join and have their play tracked on the machines in order to earn “comps” such as free food, free drinks, free shows, free gifts, invitationsto special events and more.
To track your play you are issued a card, similar to a magnetic-striped credit card, that is inserted into the machine and it will track your wins and losses, as well as the total amount of allyour bets. Naturally, the more you play on the machines, the more free stuff you will get from the casino. When deciding how much to give you back in benefits for your play, the casino mustfirst calculate your total theoretical loss to determine how much they have earned from you. Then, based on that total, they will rebate a certain percentage back to you in the form ofcomps and free play. The actual percentage rebated to the player is a trade secret for each casino but, again, it is always based on a player’s tracked theoretical loss.
I live only one mile from the Seminole Hard Rock Casino in Hollywood and I joined their Seminole Wild Card player’s club shortly after the property opened in 2004. Although I did not playmuch in the ensuing years, in late 2013 I began to play rather heavily and it continued through early 2017. My game of choice was video poker rather than slot machines because there is a skillinvolved in video poker and I used software to learn how to play my hands properly. Eventually, I played at an expert level that allowed the casino to have only a slight mathematical edge overme.


Overall, my results were pretty good as I hit quite a few royal flushes in 2016 and that helped me to come out ahead for my three years of play. In early 2017 the casino made some changes totheir video poker games, which made them less desirable, and I stopped playing. During my period of play I used that opportunity to analyze the Seminole Wild Card Player’s club and, following,is what I discovered.
The set-up of the Seminole Wild Card Player’s club is somewhat unusual because at most casinos when you play a machine you will earn points based on the total amount of money you put through amachine. On some machines it may be that $5 earns one point, while on other machines it may be $10 or $25 earns one point.
Try an online casino for FREE. We have over 15 No Deposit Bonus Codes. No credit card needed, just sign up and startplaying!
The Seminole Wild Card Player’s club is different because players don’t earn points on each machine, instead they earn comp dollars. As an example, for playing $10 through one machine you mightearn six cents, while on another machine you might only earn three cents. So, if you ended up playing $1,000 for the day on the same machine, your comps would total $6 on the first machine, or$3 on the second machine. As a player, you wouldn't really know why one machine gave more comps, but you could correctly theorize that the machines that had a higher rate meant that the casinowas making more of a theoretical win from you and that's why they could give you back more comps.
The comps you earned could then be spent like regular dollars at hotels, restaurants, bars, lounges and retail stores at any of the six Seminole Casinos. Besides earning comps, each day's playalso earned you status credits and those enabled you to reach a higher player's card level. Interestingly, there was no information on a formula for how the status credits were earned. As aplayer all you knew was that you could check your account each day to see how many status credits you earned for your previous day's play.
The player's club only has three tiers: Platinum, Elite and X Card. All players start at Platinum and to reach Elite you need to earn 3,750 status credits within a three-month period. X Card isreserved for the casino's biggest players, but there is no public information available on what is needed to attain that level.
I easily attained Elite level and after tracking the comps and status credits I earned each day, within a few months I began to realize that the status credits actually represented my totaltheoretical loss for each day. I was able to confirm this through test play on certain machines, as well as speaking with other knowledgeable players.
Once I knew that the earned status credits represented my total theoretical loss I was then able to compare that number to the total comps I earned on that same day and I realized that therewas a relationship between those two numbers. As an example, one day I earned $48.75 in comps and I was awarded 828 status credits. By multiplying $48.75 by a factor of 17 the result was828. Another day I earned $30.83 in comps and 524 status credits. Once again, by multiplying $30.83 by 17 the result was 524. That relationship was absolute and no matter what day I played, Ifound that I could always multiply the amount of my earned comps by 17 to determine my status credits (theoretical loss) for that day.
Since I now knew how to calculate my theoretical loss for the day, based on the comps I earned, I then realized that I would be able to calculate what the casino had set as its theoreticalpayback percentage for any electronic game on the floor.
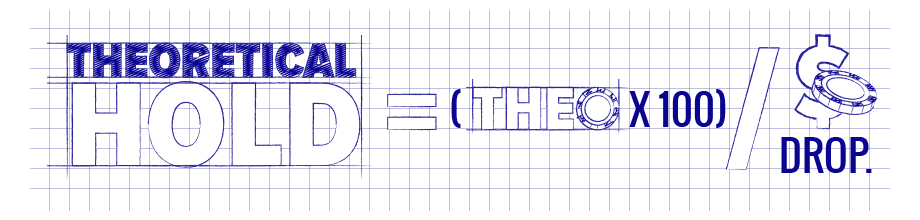
How to Calculate the Theoretical Payback Percentage on a Slot Machine - I believe that anyone can calculate the theoretical payback percentage on any gaming machine in aSeminole Casino by using a formula that I created. The key to calculating a machine’s theoretical payback percentage is to track how many comp dollars you earn for putting exactly $100 in playthrough a machine. For example, if you bet $1 a spin, just track how many comp dollars you have earned after making 100 bets. Once you know that number, you can simply multiply it by 17 and youwill know the casino’s theoretical win rate for that machine. Deduct that number from 100, and you will then know the theoretical payback for that machine.
As an example, let’s say you put $100 through a penny slot machine and you earn 54 cents in comps. Just multiply .54 x 17 and you will get 9.18, which represents the casino’s theoretical winrate for that machine - 9.18%. Then, deduct 9.18 from 100 and you get 90.82 which would represent the casino’s theoretical payback percentage for that particular machine - 90.82%.
I found this method to be accurate and I tested it on dozens of machines at four different Seminole casinos. It should also work at the other two Seminole casinos since they all share the sameplayer’s club. One word of warning, however, is that I found the method to only be accurate for single-denomination machines. If you play a multi-denomination machine the method cannot berelied upon to give you an accurate payback percentage for all of the denominations.
How Do Slot Paybacks at the Hard Rock in Hollywood Compare to the Other Local Casinos? In trying to determine an average payback percentage for slot machines at the Hard Rock in Hollywood, Irealized that it would not be possible to get an actual accounting and I would just have to make an educated guess based on the results of playing some machines in different denominations.
Therefore, I randomly played 10 different machines throughout the casino in three different denominations: pennies, quarter and dollars. As mentioned previously, I had to play exactly $100through each machine and in some instances it wasn’t possible to play exactly $100, so I might have gone over by a few pennies.
In the table below you can see the results for playing 10 random penny slots and the average theoretical return was 88.37%
| Date Played | Machine # | Name | comps earned for $100 coin-in | Theoretical Hold | Theoretical Payback |
| 30-Nov | 012714 10130 | Moon Maidens | $0.68 | 11.56% | 88.44% |
| 17-Aug | 040312 04892 | Quick Strike Mystery Rewards | 0.69 | 11.73% | 88.27% |
| 30-Nov | 010103 11114 | Desert Dawn | 0.59 | 10.03% | 89.97% |
| 17-Aug | 034106 09083 | Quick Hit Platinum | 0.64 | 10.88% | 89.12% |
| 17-Aug | 050907 10010 | Fu Dao Le | 0.69 | 11.73% | 88.27% |
| 30-Nov | 012106 11952 | Jungle Riches | 0.69 | 11.73% | 88.27% |
| 17-Aug | 013504 10609 | Super Wheel Blast Lion of Venice | 0.70 | 11.90% | 88.10% |
| 17-Aug | 013510 10618 | Wild Leprecoins | 0.70 | 11.90% | 88.10% |
| 17-Aug | 043702 08245 | Buffalo Special Edition | 0.72 | 12.24% | 87.76% |
| 14-Oct | 051502 12178 | Rumble Rumble Bison | 0.74 | 12.58% | 87.42% |
| Average | 11.63% | 88.37% | |||
In the table below you can see the results for playing 10 random quarter slots and the average theoretical return was 90.89%
| Date Played | Machine # | Name | comps earned for $100 coin-in | Theoretical Hold | Theoretical Payback |
| 30-Nov | 067510 11231 | The Enforcer | $0.45 | 7.65% | 92.35% |
| 30-Nov | 032301 32091 | Triple Double Diamond | 0.53 | 9.01% | 90.99% |
| 30-Nov | 013704 09830 | Thunder Eyes | 0.54 | 9.18% | 90.82% |
| 30-Nov | 074701 11731 | Quick Hit Platnum Plus | 0.63 | 10.71% | 89.29% |
| 30-Nov | 101406 08598 | Cash Cove | 0.49 | 8.33% | 91.67% |
| 16-Oct | 064103 09534 | Colossal Cash Grand Dragon | 0.47 | 7.99% | 92.01% |
| 16-Oct | 034708 12048 | Double Hot Fire | 0.54 | 9.18% | 90.82% |
| 16-Oct | 075307 10059 | Black Diamond | 0.59 | 10.03% | 89.97% |
| 16-Oct | 101309 09950 | Mystery Rewards Glistening Jade - Rapid Hit Fever | 0.53 | 9.01% | 90.99% |
| 30-Nov | 075305 09528 | Crystal Star | 0.59 | 10.03% | 89.97% |
| Average: | 9.11% | 90.89% | |||
In the table below you can see the results for playing 10 random dollar slots and the average theoretical return was 91.40%
| Date Played | Machine # | Name | comps earned for $100 coin-in | Theoretical Hold Hold | Theoretical Payback |
| 17-Aug | 075504 50787 | Spin & Win Instant Spin | $0.47 | 7.99% | 92.01% |
| 17-Aug | 069001 09079 | Quick Hit Platinum | 0.51 | 8.67% | 91.33% |
| 12-Oct | 069710 09348 | Wild Red Sevens | 0.44 | 7.48% | 92.52% |
| 12-Oct | 069707 09345 | Triple 777 Red Hot 3 Reels | 0.44 | 7.48% | 92.52% |
| 12-Oct | 041806 05563 | Black & White 7s | 0.47 | 7.99% | 92.01% |
| 30-Nov | 067804 10546 | Double Jackpot Lions Share | 0.59 | 10.03% | 89.97% |
| 14-Oct | 065405 10508 | Midnight Eclipse | 0.47 | 7.99% | 92.01% |
| 30-Nov | 068904 08728 | Dragons Luck | 0.59 | 10.03% | 89.97% |
| 30-Nov | 068105 10158 | Sky Rider | 0.58 | 9.86% | 90.14% |
| 16-Oct | 055307 50806 | Blazing 7s 3 Reel | 0.50 | 8.50% | 91.50% |
| Average: | 8.60% | 91.40% | |||
So, now that we have analyzed the theoretical payback percentages on these machines, how do they compare to the actual returns on slots at other South Florida casinos in those samedenominations?
Casino Theoretical Win
Well, unfortunately, Florida’s Division of Pari-Mutuel Wagering, which compiles the statistics on payback percentages for all racetrack casinos only releases information on the average payoutfor all machines within each casino and not for specific denominations. We did put in a public records request asking for a breakdown of those stats by denomination, but we received thefollowing reply: “The Division does not maintain information responsive to the following request: slot machine gaming revenue reports by denomination (one cent, nickel, quarter, dollar, etc.).”
Since we couldn’t get information on payback percentages by denomination, it was not possible to compare the Hard Rock’s machines with those at the pari-mutuels. However, it was possible tomake an educated guess about the overall returns on the Hard Rock’s machines. For the 12-month period from July 2016 through June 2017, the pari-mutuel casino with the highest average returnswas Magic City at 93.55% and the lowest returns could be found at the Isle in Pompano where they averaged 90.91%. Therefore, based on the numbers shown in the tables above, I would have toagree that the Hard Rock Hollywood’s slot paybacks are “comparable” to those at other local casinos and they are not set to pay back at the low rates that some people would suggest.
How Do Returns on Machines at The Seminole Hard Rock Casino in Tampa Compare to Returns at Casinos in South Florida? On the American Casino Guide website visitors can leave a review forany U.S. casino and the Seminole Hard Rock in Tampa has gotten almost 200 reviews - https://www.americancasinoguide.com/florida/seminole-hard-rock-hotel-a-casino-tampa.html The vast majority of those reviews are complaints about how bad the paybacks are on the slotmachines. The thinking seems to be that, once again, the machines are set to pay back at a very low rate, especially since the Tampa casino has no competition because the nearest non-Seminolecasino is about 250 miles away. That sentiment seemed somewhat logical to me so I thought I would investigate further by making a trip to Tampa to visit the casino.
I arrived late in the day and I spent a few hours that evening, as well as a few more hours the next morning testing various machines using my formula. My thought was to find some of theexact same machines I played at the Hard Rock in Hollywood and to see if the theoretical payback percentages were lower. This turned out to be harder than I expected as I found it difficult tofind the same machines in the same denominations. One other thing I noticed was that there did not seem to be too many penny slots. Instead, the vast majority of the lower denomination gameswere two-cent slots. This was not the case at the Hard Rock casino in Hollywood, where penny machines were abundant.
Eventually, I did find a few machines, in three specific denominations, that were the exact same as the ones I played in Hollywood and the table below shows how the results compared.
For penny games there were three machines I tested and, interestingly, all three had the same theoretical payback percentage as at the Hollywood Hard Rock.
| Date Played | Machine # | Name | comps earned for $100 coin-in | Theoretical Hold | Theoretical Payback | Location |
| 14-Oct | 051502 12178 | Bison Rumble Rumble | $ 0.74 | 12.58% | 87.42% | Hollywood |
| 23-Oct | 082802 05797 | Bison Rumble Rumble | $ 0.74 | 12.58% | 87.42% | Tampa |
| 17-Aug | 050907 10010 | Fu Dao Le | $ 0.69 | 11.73% | 88.27% | Hollywood |
| 23-Oct | 092206 6026 | Fu Dao Le | $ 0.69 | 11.73% | 88.27% | Tampa |
| 17-Aug | 070712 04056 | Buffalo Special Edition | $ 0.72 | 12.24% | 87.76% | Hollywood |
| 23-Oct | 043702 08245 | Buffalo Special Edition | $ 0.72 | 12.24% | 87.76% | Tampa |
Finding quarter games proved to be a bit harder. I only found two machines that were identical to ones at the Hollywood casino and, once again, the theoretical payback percentages matched upfor both casinos.
| Date Played | Machine # | Name | comps earned for $100 coin-in | Theoretical Hold | Theoretical Payback | Location |
| 16-Oct | 075307 10059 | Black Diamond | $ 0.59 | 10.03% | 89.97% | Hollywood |
| 23-Oct | 324002 30380 | Black Diamond | $ 0.59 | 10.03% | 89.97% | Tampa |
| 30-Nov | 075305 09528 | Crystal Star | $ 0.59 | 10.03% | 89.97% | Hollywood |
| 23-Oct | 015205 30371 | Crystal Star | $ 0.59 | 10.03% | 89.97% | Tampa |
At the dollar level I found four machines that matched up with their Hollywood casino counterparts. On the first one, Triple 777 Red Hot Three Reels, the comps earned were the same as at theHollywood casino. This was great because the comp rate on every machine was matching up perfectly, so far, but that soon stopped.
| Date Played | Machine # | Name | comps earned for $100 coin-in | Theoretical Hold | Theoretical Payback | Location |
| 17-Aug | 069707 09345 | Triple 7 Red Hot Three Reels | $ 0.44 | 7.48% | 92.52% | Hollywood |
| 23-Oct | 380605 50232 | Triple 7 Red Hot Three Reels | $ 0.44 | 7.48% | 92.52% | Tampa |
| 16-Oct | 055307 50806 | Blazing 7s Three Reel | $ 0.50 | 8.50% | 91.50% | Hollywood |
| 23-Oct | 040111 50330 | Blazing 7s Three Reel | $ 0.39 | 6.63% | 93.37% | Tampa |
| 17-Aug | 069001 09079 | Quick Hit Platinum | $ 0.51 | 8.67% | 91.33% | Hollywood |
| 23-Oct | 180209 50437 | Quick Hit Platinum | $ 0.41 | 6.97% | 93.03% | Tampa |
| 17-Aug | 075504 50787 | Spin And Win Instant Spin | $ 0.47 | 7.99% | 92.01% | Hollywood |
| 23-Oct | 353601 50197 | Spin And Win Instant Spin | $ 0.56 | 9.52% | 90.48% | Tampa |
On the three-reel blazing 7’s machine the comp rate was 39 cents, which would correspond to a theoretical payback percentage of 93.37%, which was higher than the 91.50% figure for the samemachine in Hollywood. A similar thing happened with the next machine I tested: Quick Hit Platinum. The comp rate on this game was 41 cents which would equal a theoretical payback percentage of93.03% which, again, was higher than the 91.33% figure for the same machine in Hollywood.
Then, on the last dollar machine I played, Spin & Win Instant Spin, the results were slightly worse. That machine gave 56 cents in comps, which would correspond to a theoretical return of90.48%, versus the same machine in Hollywood which came in at 92.01%
So, interestingly, the theoretical payback percentages for the first eight slot machines in Tampa were either equal to, or better than, the same machines in Hollywood. This was very surprisingas I thought they would be lower at the Tampa casino because they had no direct competition.
But what about all those player reviews complaining that the slots in Tampa paid less than the slots in Hollywood? Well, my research showed that the machines were set to pay back at about thesame rate in both places. However, there didn’t seem to be quite as many penny machines in Tampa, most of them were 2-cents and higher, and this could offer an explanation.
Penny machines are the most common denomination found in U.S. casinos. For example, at the two Indian casinos in Connecticut, Foxwoods and Mohegan Sun, penny machines make up about 60% of allthe slots on the floor. While I didn’t take an inventory of all the machines in Tampa I was struck by the fact that penny machines were not in abundance. Since the Tampa casino has nocompetition, it could be that they were forcing players to make a higher average bet simply by having fewer penny machines available. If so, a higher average bet would result in players losingtheir money faster, thus explaining the sour sentiments of some players. Keep in mind that the Hollywood casino would not be able to easily do the same thing because of competition from othercasinos. If a player in Hollywood didn’t think there were enough penny games available they could just go to a different casino. A player in Tampa would not have that option.
Now, looking back, it is true that one slot machine in Tampa did come in with a lower theoretical rate, but that could have simply been a mistake. Keep in mind that the casino knows what thechip in each machine is set to pay back to the public on a long-term basis and, in turn, they will set the player’s club comp rate to approximate that number. Sometimes mistakes are made andthe rate could be set too high, or too low. That could be what happened here, or perhaps it was intentional and there was a specific reason for that particular setting.
Casino Theoretical Win Equations
In conclusion, I hope that everyone reading this report understands that it is not a complete analysis of all machines at either casino. To undertake such a project would have required a hugeamount of manpower, plus a rather large bankroll to withstand the gambling losses that would be expected.
Casino Theoretical Win Equation Generator
I am just one person who set out to investigate this subject as it is my area of expertise. I have been writing about payback percentages at casinos for more than 25 years and I believe that mywork is accurate. Should anyone from Seminole casino operations want to present any further information on this subject I would welcome hearing from them. I would be also be glad to print anyrebuttal that they might want to send to me concerning this article.



